Задача о расчёте вихревых токов
Проблема вычисления влияния массивного проводящего тела (в том числе грунта) на металлоискатель, приводит нас к задаче расчёта поля вихревых токов в проводящей среде, возникающих под действием внешнего переменного магнитного поля. В нашем случае таким внешним магнитным полем мы считаем поле катушки металлоискателя. Вычислив вихревые токи, получаем возможность рассчитать создаваемое ими магнитное поле, а значит, определить влияние на катушку металлоискателя.
Для расчёта поля вихревых токов и создаваемого ими магнитного поля будем использовать следующий подход. Считаем заданным переменный ток, протекающий через катушку. Тогда мы можем вычислить магнитное поле, создаваемое катушкой в любой точке пространства - это сравнительно простая задача, хорошо изученная и в целом решённая. Магнитное поле может быть описано с помощью векторного потенциала. В общем случае, векторный потенциал, создаваемый токами в некоторой области V, рассчитывается как
$$
\def\op{\operatorname}
\begin{equation}
\vec A = \frac {\mu \mu_0} {4 \pi} \int \limits_V \frac {\vec j dV} r,
\label{a_v}
\end{equation}
$$
где V - область, в которой \( \vec j \not \equiv 0 \); r - расстояние между элементом объёма dV
и точкой, для которой вычисляется A (рис. %img:a_v).
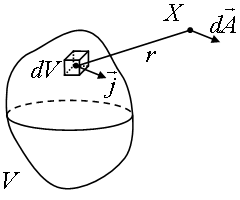
Рис. %img:a_v
На рисунке изображена область V, в которой присутствуют объёмные токи. Составляющая векторного потенциала в точке X, создаваемая бесконечно малым элементом dV с плотностью тока \(\vec j\) равна
$$
\vec{dA}=\frac {\mu \mu_0} {4 \pi} \frac {\vec j dV} r,
$$
r - расстояние между элементом объёма dV и точкой X. Для вычисления векторного потенциала поля, создаваемого областью V в целом, выполняем интегрирование по объёму V (предполагаем, что токи являются достаточно низкочастотными, чтобы можно было пренебречь запаздыванием фазы dA относительно j вследствие конечности скорости электромагнитных волн; в нашем случае это требование соблюдается)
$$
\vec A = \int \limits_V \vec{dA}
$$
и приходим к формуле \eqref{a_v}.
Если ток можно считать линейным (например, ток, протекающий по тонкому проводу катушки), то векторный потенциал в некоторой точке пространства вычисляется путём интегрирования по линии прохождения тока (по линии, проходящей вдоль провода контура или катушки)
$$
\vec A = \frac {\mu \mu_0 I} {4 \pi} \int \limits_L \frac {\vec{dl}} r,
$$
I - ток в контуре L; \(d \vec l\) - элемент контура; r - расстояние от элемента контура до точки, в которой вычисляется векторный потенциал (рис. %img:a_l).
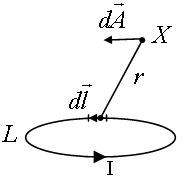
Рис. %img:a_l
На рисунке поле в точке X, создаваемое элементом контура \(\vec{dl}\)
$$
\vec{dA} = \frac {\mu \mu_0 I} {4 \pi} \frac {\vec{dl}} r,
$$
поле контура в целом получаем интегрированием
$$
\vec A = \int \limits_L \vec{dA} = \frac {\mu \mu_0 I} {4 \pi} \int \limits_L \frac {\vec{dl}} r.
$$
Впрочем, во многих случаях прибегать к интегрированию не приходится, потому как, для контуров и катушек многих форм уже выведены формулы для вычисления создаваемого ими магнитного поля.
Если в этом есть необходимость, по известному векторному потенциалу вычисляем вектор индукции магнитного поля
$$
\vec B = \op{rot} \vec A.
$$
Итак, задачу расчёта магнитного поля катушки считаем решённой. Зная магнитное поле катушки, нам требуется рассчитать поле вихревых токов в проводящем предмете (найти плотность вихревых токов как функцию от координат точки в объёме предмета). Эта задача уже гораздо более сложная, чем вычисление поля катушки. Следует иметь в виду, что переменные вихревые токи создают своё переменное магнитное поле, которое складывается с полем катушки и также влияет на распределение вихревых токов.
Для решения задачи воспользуемся уравнениями Максвелла. Нужно быть готовым к тому, что решение в аналитической форме получить не удастся и придётся довольствоваться результатами решения уравнений численными методами.
Рассчитав поле вихревых токов, получаем возможность вычислить создаваемое ими магнитное поле, а значит и суммарное магнитное поле катушки и вихревых токов. Особенно нас интересует поле в области катушки - определив изменение под влиянием предмета магнитного потока, пронизывающего катушку при заданном токе через неё, сможем определить изменение параметров катушки (индуктивности и активного сопротивления).
Далее: приступаем к выводу уравнения, описывающего поле вихревых токов, "Расчёт вихревых токов в общем случае".
author: hamper; date: 2020-02-10









