Численное решение задачи о вихревых токах при наличии осевой симметрии
Итак, мы вывели уравнение, описывающее вихревые токи в проводящем предмете, находящемся во внешнем переменном магнитном поле; получили его более простую форму для частного, но важного случая системы, обладающей осевой симметрией (проводящий предмет цилиндрической формы в магнитном поле круговой катушки, соосной с цилиндром). Теперь, собственно, перейдём к решению уравнения с использованием численных методов.
При рассмотрении задачи о вычислении вихревых токов в однородном цилиндре, находящемся в магнитном поле кругового контура с током, соосного с цилиндром (рис. %img:cyl), мы пришли к уравнению
$$
\def\op{\operatorname}
\begin{equation}
\frac {\partial^2 \dot A_e} {\partial r^2} +
\frac 1 r \frac {\partial \dot A_e} {\partial r} +
\frac {\partial^2 \dot A_e} {\partial z^2} -
\frac {\dot A_e} {r^2} \approx
i \omega \sigma \mu \mu_0 \dot A_0 +
i \omega \sigma \mu \mu_0 \dot A_e.
\label{base_eq}
\end{equation}
$$

Рис. %img:cyl
Полученное уравнение является дифференциальным уравнением в частных производных. Будем решать его численно. Для минимизации вычислений будем вычислять магнитное поле вихревых токов Ae только в точках, принадлежащих проводящему цилиндру 2. В силу того, что величина \(\dot A_e\) (как и \( \dot j, \dot A_0, \dot A = \dot A_0 + \dot A_e\)) в некоторой точке зависит только от координат (r, z) точки и не зависит от \(\theta\), достаточно вычислить Ae только в точках любого сечения цилиндра, проходящего через ось цилиндра. Ось цилиндра делит сечение цилиндра на два одинаковых прямоугольника, на две половины. Один из этих прямоугольников может быть получен из другого путём поворота на угол \(\Theta=\pi\), а значит, Ae в соответствующих точках с одинаковыми значениями координат (r, z) будут одинаковыми. То есть, достаточно вычислить Ae для точек, принадлежащих половине сечения цилиндра, чтобы полностью описать поле во всём цилиндре.
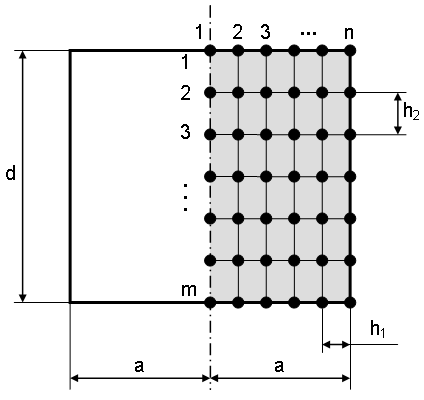
Рис. %img:grid
Разобьём прямоугольную область с помощью равномерной прямоугольной сетки (рис. %img:grid), имеющей m*n узлов (m точек по вертикали, n точек по горизонтали). Расстояние между соседними узлами по горизонтали обозначим как h1, а расстояние между соседними узлами по вертикали обозначим h2. Если радиус цилиндра равен a, а его высота равна d, то
$$
h_1=\frac a {n-1}, \\
h_2=\frac d {m-1}.
$$
Введём индексацию узлов сетки следующим образом. Горизонтальный ряд узлов будем называть строкой, строки будем нумеровать сверху вниз от 1 до m. Вертикальный ряд будем называть столбцом, столбцы будем нумеровать от 1 до n. Индексами (p, q) будем обозначать узел в строке с номером p и в столбце номер q (далее также будет введён другой способ индексации с использованием одного индекса, т.е. с последовательной нумерацией всех узлов сетки). Будем искать неизвестную величину Ae в узлах сетки, обозначим её значение в узле (p, q) как \(A_{p, q}\).
Для приближённого решения исходного дифференциального уравнения \eqref{base_eq}, заменим уравнения разностными уравнениями, которые запишем для узлов сетки.
Воспользуемся известными из математического анализа приближёнными соотношениями для вычисления производной в точке (рис. %img:grid), которые для функции одной переменной имеют вид
$$
{y''}_0 \approx \frac {y_{-1}-2y_0+y_1} {h^2}, \\
{y'}_0 \approx \frac {y_1-y_0} h,
$$
где
$$
y_0=y(x_0), \\
y_{\pm 1}=y(x_0 \pm h).
$$
При желании можно воспользоваться более сложными выражениями с более высоким порядком точности, но пока ограничимся наиболее простым вариантом.

Рис. %img:grid
Применительно к функции двух переменных, как в нашем случае, соотношения примут вид
$$
\Bigl. \frac {\partial^2 y} {\partial r^2} \Bigr|_{(p, q)} \approx
\frac {y_{p, q-1}-2y_{p, q}+y_{p, q+1}} {h_1^2}, \\
\Bigl. \frac {\partial y} {\partial r} \Bigr|_{(p, q)} \approx
\frac {y_{p, q+1}-y_{p, q}} {h_1}, \\
\Bigl. \frac {\partial^2 y} {\partial z^2} \Bigr|_{(p, q)} \approx
\frac {y_{p-1, q}-2y_{p, q}+y_{p+1, q}} {h_2^2},
$$
где y - это краткое обозначение для \(\dot A_e\). Взаимное расположение точек, значения y в которых используются в приведённых выражениях, поясняется рисунком %img:d2.

Рис. %img:d2
Теперь на основе соотношений для вычисления производных и уравнения \eqref{base_eq}, для каждого из внутренних узлов сетки можем записать следующее разностное уравнение
$$
\frac {y_{p, q-1}-2y_{p, q}+y_{p, q+1}} {h_1^2} +
\frac 1 {h_1 (q-1)} \frac {y_{p, q+1}-y_{p, q}} {h_1} + \\
+ \frac {y_{p-1, q}-2y_{p, q}+y_{p+1, q}} {h_2^2} -
\frac {y_{p, q}} {h_1^2 (q-1)^2} = \\
= i \omega \sigma \mu \mu_0 A_{0\ (p, q)} +
i \omega \sigma \mu \mu_0 y_{p, q},
$$
где \( A_{0\ (p, q)} \) - внешнее магнитное поле (поле, создаваемое контуром с током) в узле (p, q);
индексы внутренних узлов находятся в диапазонах p = 2..m-1, q = 2..n-1.
При составлении уравнений мы учли то, что координата r узла (p, q), очевидно, равна \(r=h_1 (q-1)\).
Мы получили линейные уравнения относительно неизвестных значений y (т.е. \(\dot A_e\)) в узлах сетки. Приводя подобные, перепишем уравнение в виде
$$
\begin{equation}
y_{p, q-1} \frac 1 {h_1^2} +\\
+ y_{p, q} \left( - \frac 2 {h_1^2} - \frac 1 {h_1^2 (q-1)} - \frac 2 {h_2^2} - \frac 1 {h_1^2 (q-1)^2} - i \omega \sigma \mu \mu_0 \right) + \\
+ y_{p, q+1} \left( \frac 1 {h_1^2} + \frac 1 {h_1^2 (q-1)} \right) + \\
+ y_{p-1, q} \frac 1 {h_2^2} + \\
+ y_{p+1, q} \frac 1 {h_2^2} = i \omega \sigma \mu \mu_0 A_{0\ (p, q)}.
\label{inn_eq}
\end{equation}
$$
В такой записи хорошо видно, как рассчитываются коэффициенты при неизвестных.
Всего мы имеем m*n неизвестных, по числу узлов сетки. Для нахождения неизвестных требуется составить систему из m*n независимых линейных уравнений. Поэтому уравнения \eqref{inn_eq}, составленные для внутренних узлов сетки, должны быть дополнены уравнениями для граничных точек (граничными условиями), тогда и получим требуемое количество уравнений.
Проще всего обстоит дело с границей, проходящей по оси цилиндра (левая граница прямоугольной области на рисунке %img:bound). Для точек на оси из соображений симметрии (или из самого вида уравнения \eqref{base_eq}, или из того, что A0 = 0 на оси, следовательно, на оси нулевыми будут плотности вихревых токов и Ae) можно сделать вывод о том, что
$$
\Bigl. \dot A_e \Bigr|_{r=0} = 0,
$$
что соответствует линейным уравнениям в количестве m штук:
$$
y_{p, 1}=0, \\
p=1 \dots m.
$$

Рис. %img:bound
Если бы нам было известно поле вихревых токов в рассматриваемой проводящей цилиндрической области, мы смогли бы вычислить потенциал Ae для всех оставшихся граничных точек и, тем самым, дополнить систему линейных уравнений недостающими уравнениями.
В квазистационарном приближении, при известном распределении токов, векторный потенциал вычисляется как
$$
\vec A_e = \frac {\mu \mu_0} {4 \pi} \int \limits_V \frac {\vec j dV} r,
$$
где V - та область с токами, магнитное поле Ae которых мы хотим вычислить; r - расстояние между элементом объёма dV и точкой, для которой вычисляется Ae.
Как мы установили ранее (подробнее смотрите "Расчёт вихревых токов в общем случае"), вектор плотности вихревых токов в точке может быть вычислен, если известно магнитное поле (векторный потенциал) в этой точке:
$$
\vec j = \sigma \vec E = - \sigma \frac {\partial \vec A} {\partial t} =
- \sigma \frac {\partial (\vec A_0 + \vec A_e)} {\partial t}.
$$
Или, в нашем случае для \(\theta\)-проекций в цилиндрической системе координат в комплексной форме
$$
\dot j = - i \omega \sigma (\dot A_0 + \dot A_e),
$$
тогда
$$
\begin{equation}
\dot A_e = - \frac {i \omega \sigma \mu \mu_0} {4 \pi} \int \limits_V \frac {(\dot A_0 + \dot A_e) dV} r.
\label{int_eq}
\end{equation}
$$
Получили интегральное уравнение относительно Ae.
Как известно, численное интегрирование функции сводится к суммированию её значений в некоторых дискретных точках области интегрирования, значения функции берутся с определёнными весовыми коэффициентами. То есть, заменяя в уравнении \eqref{int_eq} правую часть на сумму - приближённое значение интеграла, получаем не что иное, как линейное уравнение, в приближении заменяющее интегральное. Этими уравнениями мы и дополним нашу систему линейных уравнений, после чего сможем найти все значения неизвестных (значения y во всех узлах сетки).
Кстати, все уравнения системы могут быть получены на основе интегрального уравнения \eqref{int_eq} и при этом никаких проблем с граничными условиями не возникнет. Однако потребуется гораздо больший объём вычислений, поэтому здесь мы предпочли использовать разностные уравнения на основе дифференциального уравнения \eqref{base_eq}, где это возможно, а на основе интегрального уравнения лишь зададим граничные условия.
Итак, заменив в интегральном уравнении \eqref{int_eq} интегрирование приближением в виде суммы, получим выражение для вычисления магнитного поля вихревых токов в некоторой точке с индексом b
$$
\begin{equation}
\dot A_{e b}=\sum_k C_{b k} (\dot A_{0 k}+\dot A_{e k})=
\sum_k C_{b k} \dot A_{0 k} + \sum_k C_{b k} \dot A_{e k}
\label{ck}
\end{equation}
$$
или
$$
\begin{equation}
\dot A_{e b} - \sum_k C_{b k} \dot A_{e k} = \sum_k C_{b k} \dot A_{0 k}.
\label{int_lin}
\end{equation}
$$
Очевидно, это линейное уравнение; здесь \( \dot A_{e b} \) - величина, взятая для одной из граничных точек; \( \dot A_{e k} \) - величины, в точках цилиндра; Cb k - "весовые" коэффициенты, их значения нам пока неизвестны; для каждой точки b требуется свой набор коэффициентов (количество коэффициентов в каждом наборе равно количеству узлов сетки, m*n). Здесь мы перешли к "линейной" индексации неизвестных (или узлов), т.е. к использованию одного индекса для узлов (в отличие от индексации с двумя индексами при введении в рассмотрение сетки). Здесь "линейная" индексация удобнее. Способ последовательной нумерации узлов непринципиален и может быть любым. Желательно выбирать его так, чтобы переход от одной системы индексов к другой был простым, так как при объединении всех уравнений в общую систему, все переменные будем приводить к общей "линейной" индексации.
Заметим, что хотя уравнение \eqref{int_eq} предполагает интегрирование по объёму цилиндра, суммы мы записали только для точек - узлов сетки. Это возможно, поскольку, как мы отмечали ранее, в нашем случае поле в пределах сетки полностью описывает поле во всём цилиндре. Поэтому суммирование по точкам во всём объёме может быть заменено суммированием по узлам сетки при должном подборе "весовых" коэффициентов.
Линейные уравнения вида \eqref{int_lin} составим для каждой граничной точки b, кроме точек на оси цилиндра, для которых граничные условия уже получены. Как мы уже отмечали, для каждого из таких уравнений потребуется указать свой набор коэффициентов Cb k. Поясним, как можно найти эти коэффициенты.
Объёмные токи области в силу симметрии задачи обладают теми же свойствами, что и векторы \( \vec A_0, \vec A_e, \vec A\) (имеют только одну ненулевую проекцию, \(\theta\)-проекцию, не зависящую от \(\theta\)). Иначе говоря, линии вектора плотности тока образуют коаксиальные окружности, общая ось которых совпадает с осью проводящего цилиндра. Тогда можно предположить, что магнитное поле вихревых токов останется практически неизменным, если объёмные токи заменить некоторым множеством специально подобранных линейных токов, текущих по коаксиальным окружностям.
Выберем систему линейных (круговых) токов таким образом, чтобы каждый из токов проходил через центр некоторой ячейки нашей сетки (рис. %img:cell).

Рис. %img:cell
Будем считать, что каждый из узлов сетки, находящихся по углам некоторой ячейки, даёт вклад в круговой ток, проходящий через ячейку, равный
$$
\frac 1 4 j_{p, q} h_1 h_2.
$$
Здесь h1h2 - площадь ячейки; jp, q - плотность тока в узле сетки (p, q), угловом для рассматриваемой ячейки.
Магнитное поле, создаваемое объёмными токами в рассматриваемой области, будем считать приближённо равным магнитному полю, создаваемому линейными токами, которые мы ввели в рассмотрение. Поле кругового тока рассчитать достаточно просто, этот вопрос мы уже рассматривали в статье "Решение задачи при наличии осевой симметрии". Линейные токи ввели специально таким образом, чтобы они не проходили через узлы сетки, тогда не возникнет проблем с вычислением магнитного поля в узлах (r в \eqref{int_eq} нигде не обращается в 0).
Перейдём к вычислению коэффициентов Cb k. Если принять силу кругового тока некоторой ячейки с номером g, равной 1 А, сможем рассчитать в интересующей нас точке с индексом b векторный потенциал создаваемого током магнитного поля, обозначим его \(\theta\)-проекцию как Ac g. При заданных размерах цилиндра и заданной точке вычисления векторного потенциала b, это вполне определённое число.
Но круговой ток не обязан быть равным 1 А. Создаваемое им на самом деле поле пропорционально значению этого тока, которое мы договорились считать равным
$$
I_g = \frac 1 4 h_1 h_2 (j_{g1}+j_{g2}+j_{g3}+j_{g4}),
$$
где \(j_{gx}\) - плотности тока для узлов, являющихся угловыми для рассматриваемой ячейки g, через которую проходит круговой ток.
Тогда получаем, что поле, создаваемое ячейкой g
$$
\Delta A_{e g} = \frac 1 4 h_1 h_2 A_{c g} (j_{g1}+j_{g2}+j_{g3}+j_{g4}).
$$
Мы знаем, как выразить плотность вихревого тока через векторный потенциал в точке, для комплексных амплитуд можем записать
$$
\Delta \dot A_{e g} = -\frac 1 4 i \omega \sigma h_1 h_2 A_{c g} (\dot A_{g1}+\dot A_{g2}+\dot A_{g3}+\dot A_{g4}).
$$
Здесь \( \dot A_{g1}, \dot A_{g2}, \dot A_{g3}, \dot A_{g4} \) - проекции векторного потенциала (суммарного, с учётом и стороннего магнитного поля, и поля вихревых токов) в узлах, окружающих ячейку g.
Поле в рассматриваемой точке b может быть найдено как сумма составляющих от каждой ячейки,
$$
\dot A_{e b} = -\frac 1 4 i \omega \sigma h_1 h_2 \sum_g A_{c g} (\dot A_{g1}+\dot A_{g2}+\dot A_{g3}+\dot A_{g4}),
$$
суммирование производится по всем ячейкам. Изменим порядок суммирования, будем суммировать по всем узлам k сетки,
$$
\dot A_{e b} = -\frac 1 4 i \omega \sigma h_1 h_2 \sum_k \dot A_k (A_{ck1}+A_{ck2}+A_{ck3}+A_{ck4}),
$$
где \(A_{ck1}, A_{ck2}, A_{ck3}, A_{ck4}\) - поля, которые были бы созданы в рассматриваемой точке ячейками, соседними с узлом k, если бы через их центр протекал круговой ток силой 1 А; если узел k является граничным, то для ячеек, выходящих за пределы сетки, соответствующие значения принимаются равными нулю, \(A_{ckx}=0\).
Сравнивая с \eqref{ck}, видим, что коэффициенты Cb k рассчитываются как
$$
C_{b k} = -\frac {i \omega \sigma h_1 h_2} 4 (A_{ck1}+A_{ck2}+A_{ck3}+A_{ck4})
$$
Определив коэффициенты Cb k для граничных точек (по одному набору коэффициентов для каждой точки), получим граничные условия, которые вместе с разностными уравнениями \eqref{inn_eq} дадут нам систему линейных уравнений относительно Ae k - проекций векторного потенциала магнитного поля, создаваемого вихревыми токами в точках - узлах сетки. Решив систему, найдём эти неизвестные значения. В сумме с внешним полем A0 k в этих же точках, они дадут нам проекции векторного потенциала суммарного магнитного поля
$$
\dot A_k=\dot A_{0 k} + \dot A_{e k}.
$$
По этим величинам мы сможем определить плотность вихревых токов (\(\theta\)-проекцию) в узлах сетки как
$$
\dot j_k = -i \omega \sigma \dot A_k = -i \omega \sigma (\dot A_{0 k}+\dot A_{e k}).
$$
А зная распределение объёмных токов в проводящем предмете, сможем вычислить магнитное поле вихревых токов в любой точке пространства, а значит, сможем определить полное магнитное поле в любой точке.
В отсутствие проводящего объекта, магнитное поле создаётся только катушкой \((\vec A_0)\), а при наличии объекта, складывается из поля катушки и поля вихревых токов, т.е. \(\vec A = \vec A_0 + \vec A_e\), следовательно, поле вихревых токов - это изменение магнитного поля под влиянием проводящего предмета (цилиндра, соосного с катушкой в данном случае).
Зная, каким образом изменилось магнитное поле, можем вычислить изменение эквивалентной индуктивности катушки и её активного сопротивления. Для этого следует вычислить магнитный поток через поверхность, ограниченную витком катушки. Или, в нашем случае проще воспользоваться полученным ранее соотношением
$$
\vec E_e = - \frac {\partial \vec A_e} {\partial t},
$$
где \( \vec E_e \) - напряжённость электрического поля, создаваемого только составляющей переменного магнитного поля \( \vec A_e \) вихревых токов. ЭДС индукции, наводимая магнитным полем вихревых токов в контуре, рассчитывается интегрированием вектора напряжённости электрического поля по контуру
$$
{\mathcal E}_{e1} = \int \limits_{L1} \vec E_e \vec{dl}=
- \int \limits_{L1} \frac {\partial \vec A_e} {\partial t} \vec{dl}.
$$
Для комплексных амплитуд соотношение будет иметь вид
$$
\dot{\mathcal E}_{e1} = -i \omega \int \limits_{L1} \dot {\vec A_e} d \vec l,
$$
а с учётом того, что в нашем случае проекция векторного потенциала на направление элемента контура dl в любой точке контура одна и та же по величине, получаем
$$
\dot{\mathcal E}_{e1} = - 2 \pi i \omega a_1 \dot A_{e1},
$$
a1 - радиус витка катушки L1; \(\dot A_{e1}\) - \(\theta\)-проекция вектора \(\dot {\vec A_e}\) в любой точке на контуре - витке катушки.
Комплексное сопротивление катушки L1 равно отношению напряжения на L1 к току через неё. За счёт ЭДС, наводимой переменным магнитным полем вихревых токов, напряжение на катушке при наличии рядом проводящего предмета отличается от напряжения, когда посторонних предметов рядом нет (параметры переменного тока через катушку в обоих случаях считаем одинаковыми). Это приводит к тому, что комплексное сопротивление катушки под влиянием проводящего предмета изменяется, величина изменения
$$
\Delta \dot Z_1 = \frac {\dot U_{e1}} {\dot I_1} = - \frac {\dot {\mathcal{E}}_{e1}} {\dot I_1}, \\
\begin{equation}
\Delta \dot Z_1 = \frac {2 \pi i \omega a_1 \dot A_{e1}} {\dot I_1}.
\label{delta_z}
\end{equation}
$$
Ток \(\dot I_1\) (комплексная амплитуда переменного тока с циклической частотой \(\omega\)) здесь тот же самый, который брался для расчёта магнитного поля \(\dot {\vec A_0}\) катушки L1. Проще всего для вычислений принять его равным 1 А.
Изменение комплексного сопротивления катушки эквивалентно изменению её индуктивности и активного сопротивления. Комплексное сопротивление катушки с индуктивностью L и активным сопротивлением R
$$
\dot Z = R + i \omega L,
$$
тогда изменение комплексного сопротивления, вызванное изменением параметров катушки
$$
\Delta \dot Z = \Delta R + i \omega \Delta L.
$$
Сравнивая последнее выражение с \eqref{delta_z}, видим, что в нашем случае
$$
\Delta L_1 = \Re \frac {\Delta \dot Z_1} {i \omega} = \Re \frac {2 \pi \dot A_{e1}} {\dot I_1}, \\
\Delta R_1 = \Re \Delta \dot Z_1 = \Re \frac {2 \pi i \omega a_1 \dot A_{e1}} {\dot I_1},
$$
где \(\Re\) - действительная часть комплексного числа.
Наконец, вспомним, что мы считали катушку L1 состоящей из одного витка. Если витков несколько (n1) и они расположены достаточно плотно (сечение катушки мало по сравнению с её радиусом), можем считать, что наводимая в катушке ЭДС увеличится в n1 раз. Кроме того, магнитное поле катушки будет в n1 раз больше, что приведёт к пропорциональному увеличению вихревых токов и их магнитного поля. Таким образом, результирующий эффект в виде изменения параметров катушки будет в \(n_1^2\) раз больше, чем в случае одного витка. Это утверждение может быть строго обосновано, если повторить все выводы статьи с учётом того, что \(n_1 \neq 1\).
Более подробно с деталями предлагаемого здесь численного алгоритма можно на конкретном примере реализации, который рассматривается далее: "Решение задачи в Octave. Примеры расчётов".
author: hamper; date: 2020-02-15













