Теоретическая предельная глубина обнаружения
Довольно интересен вопрос - на какой наибольшей глубине металлоискатель способен ещё хоть что-то обнаружить? Наибольшая глубина обнаружения зависит от чувствительности металлоискателя и используемой катушки. Попробуем выяснить, каким образом...
Для любого прибора существует такая глубина, зависящая от его чувствительности, при превышении которой он в принципе не сможет обнаружить никакой предмет. Каким бы большим предмет ни был, даже если он бесконечно большой. Вычислим эту глубину.
Будем предполагать, что поиск происходит в идеальных условиях (абсолютно непроводящий и немагнитный грунт, нет каких-либо иных мешающих факторов).
Для вычисления предельной глубины, будем рассматривать изменение индуктивности катушки под влиянием предмета с бесконечно большой плоской поверхностью (рис. %img:intro). Материал будем считать либо имеющим нулевую удельную проводимость и бесконечно большую магнитную проницаемость, либо бесконечную удельную проводимость и единичную относительную проницаемость. Влияние такого предмета эквивалентно влиянию идеального плоского магнитного или электромагнитного экрана соответственно.

Рис. %img:intro
Задачу в предложенной формулировке проще всего решить с помощью метода зеркальных изображений, который разработан в электродинамике специально для подобных ситуаций с плоской бесконечной границей между двумя разными средами. Можно показать, что магнитное поле в первой среде при наличии экрана будет точно таким как в случае, если всё пространство заполнено первой средой, а вместо экрана, симметрично границе раздела двух сред, размещена точно такая же катушка с таким же по величине током (изображение действительной катушки). Ток в катушке-изображении направлен так же, как в действительной катушке, если экран магнитный (рис. %img:img1) и противоположно, если экран электромагнитный (рис. %img:img2). Поэтому определение влияния экрана на индуктивность катушки сводится к расчёту взаимной индуктивности двух одинаковых соосных катушек с расстоянием между ними 2*h, где h - расстояние от катушки до экрана (бесконечно большого предмета).
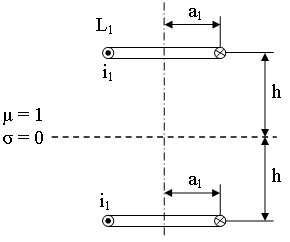
Рис. %img:img1. Изображение катушки в идеальном магнитном экране

Рис. %img:img2. Изображение катушки в идеальном электромагнитном экране
Воздействие бесконечно большого ферромагнитного объекта получается по абсолютной величине таким же, как бесконечно большого идеально проводящего объекта, но противоположным по знаку. Поэтому можно рассмотреть какой-то один случай.
Напряжение на катушке (комплексная амплитуда) рассчитывается как
$$
\dot U_1 = j \omega L_1 \dot I_1 + j \omega M \dot I_2,
$$
а с учётом того, что для случая "отражения" в идеальном экране \(\dot I_2 = \pm \dot I_1\), получаем
$$
\dot U_1 = j \omega \dot I_1 (L_1 \pm M).
$$
Знак определяется типом экрана, "+" соответствует идеальному магнитному, а знак "-" соответствует идеальному электромагнитному экрану.
Мы получили, что абсолютное изменение индуктивности катушки равно взаимной индуктивности между катушкой и её изображением,
$$
\Delta L_1 = \pm M.
$$
Взаимная индуктивность двух соосных круговых контуров одинакового радиуса a, находящихся на расстоянии x при малых значениях величины \(\gamma=2a/x\) (т.е. при достаточно большом удалении контуров друг от друга)
$$
M \approx \frac {\mu_0 \pi a} {16} \gamma^3 \left( 1 - \frac 3 4 \gamma^2 + \frac {75} {128} \gamma^4 - \frac {245} {512} \gamma^6 + \dots \right)
$$
(подробнее о вычислении индуктивностей и взаимных индуктивностей различных катушек смотрите в [%link:calc_l]). Считая размеры поперечного сечения катушки малыми по сравнению с размерами катушки, а бесконечно большой объект (или экран) достаточно удалённым, ограничимся первым членом ряда. С учётом того, что катушка содержит n1 витков, получаем
$$
|\Delta L_1| = M \approx \frac {\mu_0 \pi n_1^2 a_1^4} {16 h^3}, \\
|\varepsilon_{L1}| = \frac {|\Delta L_1|} {L_1},
$$
здесь мы также учли, что расстояние между катушкой и её изображением в 2 раза больше расстояния между катушкой и экраном, x=2*h. Индуктивность катушки мы оценивали как \(L_1 \approx 4.242 \mu_0 n_1^2 a_1\), тогда для отклика на бесконечно большой объект получаем значение
$$
\begin{equation}
|\varepsilon_{L1}| \approx \frac {a_1^3} {21.60 h^3}.
\label{eps_for_inf}
\end{equation}
$$
Если для объектов конечных размеров мы получали, что величина отклика обратно пропорциональна 6-й степени глубины (при достаточно большой глубине), то для бесконечно большого объекта имеем обратную пропорциональность 3-й степени глубины, что означает значительно более медленное уменьшение отклика с глубиной.
Обозначив через p порог чувствительности прибора (минимальный отклик, который прибор способен обнаружить), можем из соотношения \eqref{eps_for_inf} выразить максимальную глубину, на которой может быть обнаружен бесконечно большой объект
$$
\begin{equation}
h_{max} \approx \frac {a_1} {\sqrt[3]{21.60 p}}.
\label{hmax}
\end{equation}
$$
Подсчёт для разных значений p даёт следующие результаты
| p |
10-4 |
10-5 |
10-6 |
10-7 |
| hmax |
7.7*a1 |
17*a1 |
36*a1 |
77*a1 |
Напомним, что чувствительностью порядка 10-4 обладает металлоискатель "на биениях"; величина 10-5 типична для неплохого прибора на основе цифрового измерения частоты; чувствительность порядка 10-6 способен продемонстрировать хороший индукционный металлоискатель; 10-7 - это очень хороший показатель для очень хорошего прибора.
Полученные оценки оказываются избыточно оптимистичными - для очень хороших металлоискателей с катушкой диаметром около 30 см теоретическая предельная глубина поиска оказывается в районе 10 м.
На самом деле на таких глубинах, даваемых формулой \eqref{hmax}, ничего обнаружить не получится, даже в идеальных условиях, без влияния грунта. И не только потому, что отклик на реальный очень большой объект меньше, чем на бесконечно протяжённый. Даже если объект в действительности был бы бесконечно большим, обнаружить его не удалось бы - отклик на него при указанной глубине оказывается не только предельно слабым, но и статичным, т.е. не изменяющимся по величине при перемещениях катушки в горизонтальной плоскости. Так что подобный отклик неотличим от смещения "нуля" прибора и должен быть отфильтрован.
Рассмотрим другую оценку максимальной глубины поиска. Поскольку отклик на бесконечный объект не изменяется при перемещении катушки в горизонтальной плоскости, предположим, что для его обнаружения будем перемещать катушку по вертикали. Если при перемещении катушки по вертикали на расстояние x, отклик изменяется на величину, хотя бы равную порогу чувствительности прибора p, то объект может быть обнаружен. С учётом \eqref{eps_for_inf}, запишем
$$
p = |\Delta \varepsilon_{L1}| \approx \frac {3 a_1^3} {21.60 h_{max}^4} x \approx
\frac {a_1^3} {7.20 h_{max}^4} x,
$$
тогда максимальная глубина обнаружения
$$
h_{max} \approx \sqrt[4]{\frac {a_1^3 x} {7.20 p}}.
$$
Если зададимся значениями a1 = 0.1 м и x = 0.1 м, то получим следующие значения предельной глубины для приборов с различной чувствительностью:
| p |
10-4 |
10-5 |
10-6 |
10-7 |
hmax, м
(a1 = x = 0.1 м) |
0.61 |
1.1 |
1.9 |
3.4 |
%link:calc_l. "Калантаров П. Л., Цейтлин Л. А. Расчёт индуктивностей: Справочная книга (3-е изд.), 1986.
author: hamper; date: 2020-01-30






