Частота сигнала. Измерение частоты. Мгновенная и средняя частота
Частота f сигнала - величина, обратная его периоду T:
$$
f = 1 / T.
$$
Из определения следует, что частота численно равна количеству колебаний (количеству периодов) в единицу времени.
Понятия частоты и периода применимы, строго говоря, только к периодическим сигналам (функциям). Для заданной периодической функции, частота и период - постоянные величины.
Реальные сигналы не идеальны, они никогда не бывают строго периодическими. Тем не менее, по отношению к реальным сигналам также используется понятие частоты. Что понимают под частотой в этом случае?
Оглавление
Частота сигнала. Измерение частоты. Мгновенная и средняя частота
Смотрите также
Частота - важный параметр сигнала. Существует огромное множество случаев, когда необходимо знать частоту сигнала, или иметь возможность измерить частоту с высокой точностью (с целью тестирования, диагностики устройств и поиска неисправностей; для выполнения измерений в таких измерительных системах, где используется преобразование величин в частоту сигнала и т.д.). Очень часто требуется генерировать сигнал с нужной частотой: многие устройства содержат в себе генераторы опорного сигнала, от точности установки и стабильности частоты которых, зависит нормальная работа устройств. Например, очень жёсткие требования предъявляются к передатчикам (которые не должны мешать соседям по диапазону). Но и в приёмнике частота гетеродина также должна быть точно установлена и стабильна, от этого зависит точность настройки на передатчик и качество приёма. От качества опорного генератора напрямую зависит точность многих приборов (таких, например, как цифровые частотомеры или, скажем, обычные часы).
Но что это такое - частота? Рассмотрим подробнее этот вопрос.
Как уже было отмечено в самом начале, понятия периода и частоты применимы только к периодическим* сигналам (или функциям). Функция u(t) называется периодической, если существует число T > 0 такое, что для любого t
$$
u(t \pm T) = u(t),
$$
значение T называют периодом функции.
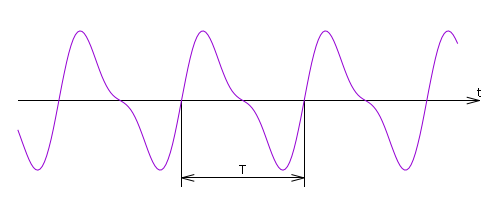
Рис. %img:pf
Понятно, что при таком определении периодическая функция имеет бесконечно много периодов: если некоторая величина является периодом функции, то и любая кратная ей величина также будет периодом. Но если периодическая функция - не константа, то для неё существует наименьший период (наименьшая положительная величина, являющаяся периодом). Далее под периодом будем подразумевать именно наименьший период.
* В математике также рассматриваются "почти периодические" функции, но это весьма специфический вопрос и в математике этим термином обозначается не совсем то, что имеется в виду под "почти периодическими" функциями в технике.
Частота периодического сигнала (функции) - величина, обратная его периоду:
$$
f = 1 / T.
$$
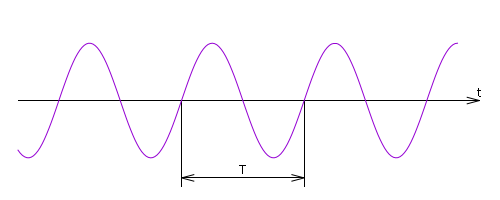
Рис. %img:hf
Примером периодического сигнала является гармонический (синусоидальный) сигнал (рис. %img:hf). Для того чтобы полностью описать такой сигнал, достаточно задать всего три параметра: амплитуду сигнала A, период T (или, что равнозначно, частоту f) и начальную фазу \( {\phi}_0 \),
$$
u(t)=A \sin \left( \frac {2 \pi} T t + {\phi}_0 \right).
$$
Запишем то же самое с использованием частоты:
$$
u(t) = A \sin( 2 \pi f t + {\phi}_0).
$$
Наряду с частотой сигнала, также рассматривается циклическая (также иногда называемая круговой или угловой) частота \( \omega = 2 \pi f \), используя которую, выражение для синусоидального сигнала можем записать следующим образом:
$$
u(t) = A \sin( \omega t + {\phi}_0).
$$
Иногда слово "циклическая" опускают, если из контекста или обозначений понятно, о какой именно частоте идёт речь.
Последнее выражение можно записать ещё проще:
$$
u(t) = A \sin \phi(t),
$$
где \( \phi(t) = \omega t + {\phi}_0 \) - фаза сигнала. Нетрудно заметить, что фаза синусоидального сигнала линейно растёт со временем. Со скоростью, равной циклической частоте:
$$
\frac {d \phi} {dt} = \omega,
$$
откуда можем выразить частоту через фазу (фаза рассматривается как функция времени)
$$
\omega = \frac {d \phi} {dt}, \\
f = \frac {\omega} {2 \pi} = \frac 1 {2 \pi} \frac {d \phi} {dt}.
$$
Как и в случае любого периодического сигнала, частота синусоидального сигнала является константой.
Строгие определения и формальные теоретические подходы хороши для математики. В реальной жизни, в технике, сигналы никогда не бывают периодическими. Прежде всего, потому что никакой сигнал не может длиться бесконечно долго. Сигнал имеет начало и конец, что уже нарушает идеальную периодичность. Но даже если отвлечься от этого, скорее философского вопроса о конечности существования, то и за время существования сигнала, строгая периодичность недостижима. С другой стороны, некоторая степень регулярности и повторяемости характерна для очень многих реальных сигналов.
Часто такие сигналы оказывается удобно представлять в квазигармонической форме
$$
\begin{equation}
u(t)=A(t) \sin \phi (t),
\label{qharm}
\end{equation}
$$
где в отличие от гармонического сигнала (т.е. сигнала вида \( u(t)=A \sin \omega t \)), амплитуда A(t) уже не обязательно постоянна, а фаза \( \phi(t) \) не обязана линейно изменяться со временем.
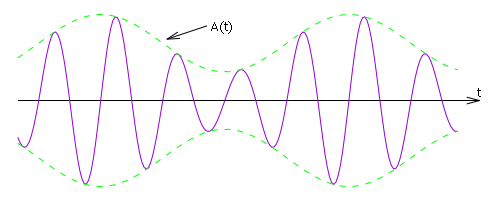
Рис. %img:cf
Функция A(t) описывает поведение огибающей сигнала. Фаза \( \phi(t) \) определяет поведение сигнала в пределах "периода" и "повторяемость" сигнала. В частности, фаза определяет моменты прохождения сигнала через 0: если \( \sin \phi = 0 \), то понятно, что и \( u(t) = 0 \); это происходит, когда
$$
\phi (t) = k \pi,
$$
где k - целое.
Мгновенной частотой такого квазигармонического сигнала, по аналогии с гармоническим, называют скорость изменения его фазы:
$$
\omega = \frac {d \phi} {dt}.
$$
Мгновенная частота реального сигнала - это уже не постоянная величина, а функция времени.
Заметим, что даже в случае периодических с математической точки зрения, идеальных сигналов, иногда бывает удобнее рассматривать их как "не вполне" периодические, с изменяющейся во времени амплитудой и/или частотой.
Простейший пример - модулированный по амплитуде сигнал при модуляции его гармоническим сигналом:
$$
u(t) = A (1 + m \sin \Omega t) \sin \omega t,
$$
предполагаем, что \( \Omega \ll \omega \). Для простоты начальные фазы считаем равными 0.
Очевидно, что период \( T = 2 \pi / \omega \) несущего колебания уже не является периодом модулированного сигнала из-за множителя \( (1 + m \sin \Omega t) \), который изменится через время T.
Легко показать, что если частота несущего сигнала кратна частоте модулирующего сигнала, т.е.
$$
\omega = k \Omega,
$$
k - целое, то период модулированного сигнала оказывается равным периоду модулирующего. Если частоты не кратны, но соизмеримы (их отношение выражается рациональным числом), то период сигнала оказывается ещё больше, он будет в целое количества раз больше периода низкочастотного модулирующего колебания. А если частоты несоизмеримы (их отношение не является рациональным числом), то модулированный сигнал, строго говоря, оказывается непериодическим.
Излишне говорить, что с практической точки зрения такой подход совершенно неудобен; истинные частота и период рассмотренного сигнала абсолютно не отражают его реальных свойств. В то же время, мгновенная частота, которая в случае амплитудно-модулированного сигнала равна частоте несущего сигнала \( \omega \), оказывается намного более объективной и информативной характеристикой сигнала.
Перейдём теперь к вопросу об измерении частоты. В общем случае, измерение мгновенной частоты сигнала - достаточно сложная задача. Она заметно упрощается, когда заранее имеется информация о характере сигнала (известен вид функции, описывающей сигнал). Тогда, отслеживая мгновенные значения сигнала и обрабатывая эти данные (с помощью аналоговой цепи или цифровыми методами), сможем определять мгновенную частоту сигнала в любой момент. Получаемая при этом точность, по ряду причин, часто оказывается не слишком высокой.
Очень точному измерению поддаётся среднее значение частоты сигнала, об этом далее.
Пусть мы имеем сигнал вида
$$
u(t)=A(t) \sin \phi (t),
$$
где A(t) > 0. Тогда точки, в которых сигнал проходит через нулевые значения, определяются только фазой. Возьмём две последовательные точки t1 и t2 такие, что в этих точках
$$
\sin \phi(t) = 0,
$$
а значит и
$$
u(t) = 0,
$$
причём u(t) проходит через нулевое значение в этих точках в одном направлении. Например, от отрицательных значений к положительным (рис. %img:mf). Это означает, что \( \sin' \phi \) в этих точках имеет одинаковый знак, в нашем случае - оба значения положительные.
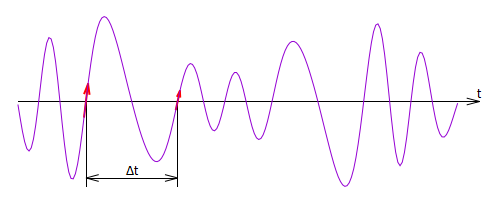
Рис. %img:mf
С учётом свойств периодичности тригонометрических функций, можем утверждать, что значения фазы в указанных точках отличаются на \( 2 \pi \):
$$
\phi(t_2) - \phi(t_1) = 2 \pi.
$$
Так как мгновенная циклическая частота \( \omega = d \phi / dt \), то эта же разность фаз может быть вычислена интегрированием мгновенной частоты:
$$
\phi(t_2) - \phi(t_1) = \int_{t_1}^{t_2} \frac {d \phi} {dt} dt = \int_{t_1}^{t_2} \omega dt.
$$
А так как \( \phi(t_2) - \phi(t_1) = 2 \pi \), то и
$$
\int_{t_1}^{t_2} \omega dt = 2 \pi.
$$
Далее воспользуемся тем, что интегрирование функции и нахождение её среднего - взаимосвязанные операции. По определению, среднее значение x на отрезке [t1, t2] равно
$$
\bar{x} = \frac 1 {\Delta t} \int_{t_1}^{t_2} x dt, \\
\Delta t = t_2 - t_1.
$$
Тогда среднее значение циклической частоты
$$
\bar{\omega} = \frac 1 {\Delta t} \int_{t_1}^{t_2} \omega dt = \frac {2 \pi} {\Delta t}.
$$
Среднее значение частоты
$$
\bar f = \frac {\bar \omega} {2 \pi} = \frac 1 {\Delta t}.
$$
Получили что для того, чтобы измерить среднее значение частоты, достаточно измерить промежуток времени между двумя моментами, когда сигнал проходит через нулевое значение (в одном направлении). Впрочем, этот результат вполне соответствует интуитивному представлению о периоде реального сигнала и соотношению между периодом и частотой.
Если сигнал высокочастотный, то интервал \( \Delta t \) становится очень малым и, его оказывается трудно измерить с высокой точностью. Тогда оказывается выгодным взять интервал, за который фаза сигнала возрастает не на \( 2 \pi \), а на кратное этой величине значение, т.е \( 2 \pi m \), где m - целое:
$$
\Delta \phi = 2 \pi m.
$$
Иначе говоря, измеряем длительность не одного периода сигнала, а длительность m периодов. Тогда средняя частота за соответствующий интервал времени составит
$$
\bar f = \frac 1 {2 \pi \Delta t} \int_{t_1}^{t_2} \omega dt = \frac {2 \pi m} {2 \pi \Delta t}, \\
\bar f = \frac m {\Delta t}.
$$
Интервал измерения \(\Delta t \) по-прежнему зависит от периода сигнала, но теперь, изменяя m, можем влиять на длительность интервала, приближая его с большей или меньшей точностью к желаемому значению.
Для точного измерения \( \Delta t \) хорошо подходят цифровые методы. Покажем, как выполнить измерение. Преобразуем исходный сигнал в цифровой таким образом, что значениям \( u(t) \lt 0 \) будет соответствовать логический 0, а значениям \( u(t) \ge 0 \) - логическая 1 (рис. %img:df). Тогда моментам перехода исходного сигнала через 0 от отрицательных значений к положительным, будут соответствовать фронты полученного цифрового сигнала.
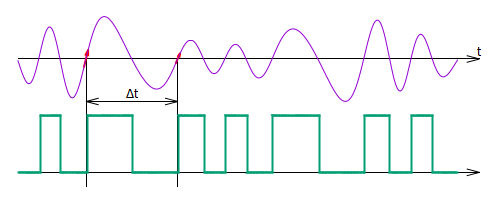
Рис. %img:df
На самом деле, обязательно наличие гистерезиса при преобразовании (порог переключения от 0 к 1 должен быть выше, чем порог обратного переключения). В противном случае, вблизи порога переключения будем получать пачки паразитных импульсов из-за наличия шумов и помех в сигнале. Но это детали реализации, не изменяющие самого принципа.
Задача определения промежутка времени между двумя заданными фронтами решается очень просто - с помощью счётчика подсчитывается количество импульсов n эталонного генератора с частотой fr (с периодом Tr) за этот промежуток времени (по первому фронту сигнала счёт запускается, по последнему - останавливается). Тогда
$$
\Delta t = n T_r = n / f_r, \\
\bar f = \frac m {\Delta t} = f_r \frac m n.
$$
Целое значение m задаётся точно. Подсчёт n выполняется с точностью \( \pm 1 \), поэтому относительная погрешность счёта, а значит и погрешность измерения \( \bar f \) составляет 1 / n (без учёта погрешности эталонного генератора). Для получения как можно меньшей относительной погрешности выгодно, чтобы значение n было как можно больше. Увеличивать n можно, увеличивая частоту эталонного генератора. Однако, на этом пути имеются ограничения, связанные с предельным быстродействием счётчика. Другой вариант - увеличивать длительность интервала измерения, увеличивая m. Этот подход позволяет достичь очень высокой точности измерений, но ценой увеличения длительности измерения.
Мы нашли способ определения средней частоты сигнала за некоторый интервал времени с высокой точностью. Но если частота сигнала изменяется, средняя частота даёт слишком мало информации о сигнале. Зачастую бывает необходимо знать, как во времени изменяется мгновенная частота сигнала и насколько сильно она отклоняется от среднего значения.
Рассмотрим, как соотносятся средняя и мгновенная частота на примере сигнала, модулированного по частоте гармоническим сигналом:
$$
\omega = {\omega}_0 + \Delta \omega \sin \Omega t.
$$
Здесь
\( \omega \) - мгновенная частота модулированного сигнала;
\( {\omega}_0 \) - его средняя частота;
\( \Delta \omega \) - наибольшее отклонение мгновенной частоты от среднего значения;
\( \Omega \) - частота модулирующего гармонического сигнала.
Для простоты считаем, что начальная фаза модулирующего воздействия равна 0.
Так как мгновенная частота по определению \( \omega = d \phi / dt \), то фаза модулированного сигнала описывается выражением
$$
\phi = \int \omega dt = \int ({\omega}_0 + \Delta \omega \sin \Omega t) dt =
{\omega}_0 t - \frac {\Delta \omega} {\Omega} \cos \Omega t + {\phi}_0,
$$
а сам сигнал может быть представлен в следующей форме
$$
u(t) = A \sin \left( {\omega}_0 t - \frac {\Delta \omega} {\Omega} \cos \Omega t + {\phi}_0 \right),
$$
впрочем, в данном случае это не столь важно.
Посмотрим, какой результат даст измерение средней частоты сигнала
$$
\bar \omega = \frac 1 {\Delta t} \int_{t_1}^{t_2} \omega dt = \\
= \frac 1 {\Delta t} \int_{t_1}^{t_2} ({\omega}_0 + \Delta \omega \sin \Omega t) dt = \\
= {\omega}_0 - \frac {\Delta \omega} {\Omega \Delta t} (\cos \Omega t_2 - \cos \Omega t_1),
$$
где \( \Delta t = t_2 -t_1 \).
Учитывая, что
$$
\cos \alpha - \cos \beta = -2 \sin \frac {\alpha - \beta} 2 \sin \frac {\alpha + \beta} 2,
$$
получаем
$$
\bar \omega = {\omega}_0 + \frac {2 \Delta \omega} {\Omega \Delta t} \sin \frac {\Omega \Delta t} 2 \sin \frac {\Omega (t_1 + t_2)} 2.
$$
Величина
$$
\frac {t_1 + t_2} 2
$$
есть не что иное, как середина интервала измерения. Это значение можно преобразовать к виду
$$
\frac {t_1 + t_2} 2 = \frac {2 t_2 - (t_2 - t_1)} 2 = t_2 - \frac {\Delta t} 2.
$$
Преобразовали выражение таким образом, чтобы этот момент времени выражался через t2, т.е. тот момент времени, когда становятся известны результаты измерения.
Тогда
$$
\bar \omega = {\omega}_0 + \frac {2 \Delta \omega} {\Omega \Delta t} \sin \frac {\Omega \Delta t} 2 \sin \Omega \left( t_2 - \frac {\Delta t}2 \right).
$$
Заметим, что если частота изменяется не по гармоническому закону, всё равно, мгновенную частоту как функцию можно разложить на гармонические составляющие и рассматривать воздействие операции усреднения на каждую составляющую по отдельности. Это возможно, поскольку операция усреднения является линейной.
Рассмотрим, как влияет интервал измерения на результат измерений. Предположим сначала, что частота сигнала изменяется достаточно медленно, а интервал измерения достаточно мал, так что
$$
\frac {\Omega \Delta t} 2 \ll 1,
$$
а значит,
$$
\sin \frac {\Omega \Delta t} 2 \approx \frac {\Omega \Delta t} 2
$$
и
$$
\bar\omega \approx {\omega}_0 + \Delta \omega \sin \Omega \left( t_2 - \frac {\Delta t} 2 \right).
$$
То есть, если выбран достаточно малый интервал измерений, то результат измерений приближается к мгновенной частоте сигнала в момент, соответствующий середине интервала измерения (результат измерения запаздывает на \( \Delta t /2 \) относительно мгновенной частоты).
С увеличением интервала измерения уменьшается коэффициент
$$
\frac {2 \Delta \omega} {\Omega \Delta t},
$$
при этом в силу свойств тригонометрических функций,
$$
\left| \sin \frac {\Omega \Delta t} 2 \right| \le 1.
$$
Так что, при
$$
\Delta t \rightarrow \infty, \bar \omega \rightarrow {\omega}_0.
$$
На основе полученных выводов можем должным образом выбрать интервал измерения.
1. Если хотим точно измерить среднюю частоту, влияние отклонений мгновенной частоты на результат необходимо минимизировать. Как было выяснено, для этого следует увеличивать интервал измерения. Предположим, что относительная погрешность метода составляет \( \varepsilon \). Тогда, вероятно, мы захотим, чтобы дополнительная погрешность, вносимая колебаниями частоты, не превышала этой величины:
$$
\frac {2 \Delta \omega} {\Omega \Delta t {\omega}_0} \lt \varepsilon,
$$
откуда получаем
$$
\Delta t \gt \frac {2 \Delta \omega} {\Omega {\omega}_0 \varepsilon}
$$
или
$$
\Delta t \gt \frac {\Delta f} {\pi F f_0 \varepsilon}.
$$
Пример. Пусть имеем сигнал со средней частотой f0 = 1 МГц, мгновенная частота которого периодически отклоняется от среднего значения на величину \( \Delta f \) до 10 Гц; желаемое относительное отклонение результата от среднего значения \( \varepsilon \lt 10^{-8} \). В зависимости от частоты F, с которой изменяется мгновенная частота f сигнала, выбираем интервал измерения, например:
$$
F = 1 \text{ Гц}: \Delta t \gt 320 \text{ с}; \\
F = 50 \text{ Гц}: \Delta t \gt 6.4 \text{ с}; \\
F = 1 \text{ кГц}: \Delta t \gt 0.32 \text{ с}.
$$
2. Предположим, что наоборот, требуется отследить изменения мгновенной частоты сигнала. Тогда имеет смысл выбирать малый интервал измерения. Прежде всего, чтобы обнаружить изменение частоты сигнала, которое происходит с частотой \( \Omega \), следует выбрать
$$
\Delta t \lt \frac {2 \pi} {\Omega} = \frac 1 F,
$$
тогда можно быть уверенным, что измеряемые отклонения не окажутся нулевыми за счёт множителя \( \sin( \Omega \Delta t / 2) \).
А если, допустим,
$$
\Delta t = \frac 1 {2 F},
$$
то
$$
\bar \omega = {\omega}_0 + c \Delta \omega \sin \left( t_2 - \frac {\Delta t} 2 \right),
$$
где коэффициент \( c \approx 0.64 \), т.е. измеряемое отклонение частоты от среднего значения составит не менее 60% от реального отклонения.
Если идёт речь о достижении как можно более высокой точности в измерении мгновенной частоты, то следует далее уменьшать интервал измерения. С уменьшением интервала, результат всё более приближается к мгновенной частоте, т.е. уменьшается динамическая погрешность измерения, но одновременно с этим растёт погрешность метода. Это ограничивает предельную точность измерения частоты путём измерения средней частоты сигнала. Не имеет смысла снижать абсолютную динамическую погрешность \( {\Delta}_2 \) до значений меньше абсолютной погрешности метода \( \Delta_1 \).
Погрешность метода (относительная и абсолютная)
$$
\varepsilon = \frac 1 n = \frac 1 {\Delta t f_r}, \\
{\Delta}_1 = \varepsilon f_0 = \frac {f_0} {\Delta t f_r}.
$$
Под динамической погрешностью будем понимать разность между наибольшим действительным отклонением \( (\Delta \omega \) или \( \Delta f) \) мгновенной частоты от среднего значения и наибольшим отклонением результата измерения от истинного значения средней частоты. Для циклической частоты погрешность может быть вычислена как
$$
\Delta \omega - \frac {2 \Delta \omega} {\Omega \Delta t} \sin \frac {\Omega \Delta t} 2
$$
или просто для частоты:
$$
{\Delta}_2 = \Delta f - \frac {\Delta f} {\pi F \Delta t} \sin(\pi F \Delta t).
$$
При малых значений аргумента, синус может быть приближённо вычислен по формуле
$$
\sin x \approx x - \frac {x^3} 6.
$$
Тогда
$$
\Delta_2 \approx \Delta f - \Delta f + \frac {\Delta f} {\pi F \Delta t} \frac {(\pi F \Delta t)^3} 6, \\
\Delta_2 \approx \frac {\pi^2 \Delta f F^2 \Delta t^2} 6,
$$
а так как мы требуем, чтобы
$$
\Delta_2 \ge \Delta_1,
$$
то можем записать
$$
\frac {\pi^2 \Delta f F^2 \Delta t^2} 6 \ge \frac {f_0} {\Delta t f_r}, \\
\Delta t \ge \sqrt[3] {\frac {6 f_0} {\pi^2 \Delta f F^2 f_r}}.
$$
Понятно, что интервал измерения при этом не может быть меньше периода сигнала (что следует из самого принципа измерения).
Пример. Сигнал имеет среднюю частоту f0 = 100 кГц, мгновенная частота отклоняется от среднего значения на величину \( \Delta f = 1 \text{ Гц} \), причём отклонение описывается синусоидой с частотой F = 10 Гц. Требуется определить оптимальный интервал измерения (при котором погрешность метода достигает динамической погрешности измерения), если частота опорного генератора составляет fr = 24 МГц. Вычисления по приведённой выше формуле дают результат \( \Delta t \approx 0.03\text{ с} \) (абсолютная погрешность метода измерения и динамическая погрешность при этом оказываются порядка 0.14 Гц).
Другим простым, но представляющим интерес примером, является измерение средней частоты сигнала, мгновенная частота которого на некотором интервале изменяется линейно. Легко показать (настолько легко, что подробно не будем на этом останавливаться), что результат будет равен мгновенной частоте в момент, соответствующий середине интервала измерения, или, что то же самое, среднему арифметическому мгновенных частот на концах интервала измерения.
Смотрите далее пример простого частотомера с хорошими характеристиками:
Частотомер на основе микроконтроллера STM32 с конвейерным измерением частоты - 2 
Особенно хотелось бы отметить книгу "Сигналы, помехи, ошибки...". Это замечательная книга, в которой хорошо раскрывается понятие мгновенной частоты; поясняется, в каких случаях уместно говорить о частоте сигнала, а когда следует переходить к рассмотрению спектра, а также подробно обсуждаются многие другие вопросы. Материал излагается довольно живо, доступно, но не упрощённо. И что приятно, книга не лишена тонкого ненавязчивого юмора.
В математических энциклопедиях можно найти определения базовых понятий (периодическая функция; почти периодическая функция; период; частота).
В энциклопедии по физике также можно найти аналогичные определения периодичности, периода, частоты и т.д.
- Финк Л. М. Сигналы, помехи, ошибки... Заметки о некоторых неожиданностях, парадоксах и заблуждениях в теории связи. М.: Радио и связь, 1984
- Математический энциклопедический словарь. /Ю. В. Прохоров. М.: Сов. энциклопедия, 1988
- Физический энциклопедический словарь. /А. В. Прохоров. М.: Сов. энциклопедия, 1983
hamper, 2021-04-06





